AB实验系统设计
一、问题场景
在产品开发,通常会有这样的场景:
- 投放这个特效,用户更愿意购物,还是不投放这个特效,用户更愿意购物?
- 这个按钮用红色,男生用户更愿意点击,还是用绿色,男生用户更愿意点击?
- 优惠券面额满300减30,新用户更愿意下单,还是满100-10,新用户更愿意下单?
问题可以归纳为:为了达成某个目标,有多种方案可以选择时,如何进行决策?
正确的做法是数据驱动,让用户来体验,看他们是用手点赞还是用脚投票,帮助进行决策。
二、核心模型
可以利用“A/B实验”来完成这个过程,A/B实验就是:为了优化某个指标,存在多种方案,在同一时间将用户流量对应分成几组,且保证每组用户特征相同的前提下,让用户分别看到不同的方案,根据几组用户的真实数据反馈,帮助产品进行决策。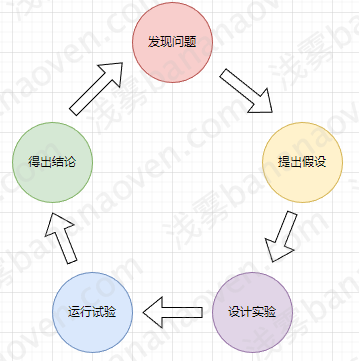
一次完整的AB实验应该包含如下5个步骤:
- 发现问题:投了那么多优惠券,为什么下单的人这么少?
- 提出假设:假设是因为优惠券面额太小
- 设计实验:确定要针对什么人群,确定实验桶的个数,每个桶投放不同的优惠券
- 运行实验:先投放较小但足够的流量,观察下单这个指标,并逐步调整流量以使指标变
化更明显。同时也要注意观察卸载APP等护栏指标,用户用脚投票可能不只是不下单,
而是卸载APP,发现问题立刻回滚并中止实验。 - 得出结论:在运行一段时间后,就可以从数学上得出结论,如有99.5%的把握,发
300-30的优惠券比100-10的优惠券更吸引人下单,那就可以做出决策一一发300-30
的优惠券。当然,如果实验结论恰好是那0.5%的错误结论,你可能做出错误的决策,
但这个概率明显低于你拍脑袋决定用哪张优惠券的犯错概率。
三、数学原理
AB实验数学上核心要做的事情是:对于给定的假设,我们能以多高的置信度去接受它。
确定抽样分布
根据中心极限定理,当抽样次数足够大时,抽样得到的分布服从正态分布。
抽样定理:均值为\(\mu\),方差为\(\sigma^2\)(有限)的任意一个总体中抽取样本量为n的样本,当n充分大时,样本均值X的抽样分布近似服从均值为\(\mu\),方差为\(\frac{\sigma^2}{n}\)的正态分布。
这里注意:
(1)总体本身的分布,不要求是正态分布。假设总体是掷骰子得到的点数,是平均分布,
但是抽样得到的分布仍然是正态分布。这个特性对于AB实验很方便,对总体没有任何约
束。
(2)抽样的样本数量需要足够大。在AB实验时,必须要对“最小样本量”进行预估,如果
低于“最小样本量”,则结果是不可信的,做实验没有意义。
这样,我们只需要研究抽样分布,就能对总体做出估计。
假设检验
1、提出假设:提出一个原假设和备择假设
- 原假设\(H_0\):收集证据予以反对的假设,通常为\(\mu_1=\mu_2\)
- 备择假设\(H_1\):收集证据予以支持的假设,通常为\(\mu_1\neq\mu_2\),根据情况,还可以是>或<
例如,我们的问题是“投了那么多优惠券,为什么下单的人这么少?”,猜测是“优惠券面额太小不够吸引用户”,于是针对“300-30”和“100-10”做实验,预期的结果是“300-30下单的用户比100-10的用户更多”。为了得到这个结论,我们需要用抽样数据估计两个实验桶的“下单用户量均值”并进行比较。
所以:
- 原假设:100-10下单数量总体均值\(\mu_1\)=300-30下单数量总体均值\(\mu_2\)
- 备择假设:100-10下单数量总体均值\(\mu_1\)<300-30下单数量总体均值\(\mu_2\)
2、做出检验
我们有很多工具能对假设进行检验:
| 检验方法 | 条件 | 目的 |
|---|---|---|
| U检验(Z检验) | - 大样本(样本容量>30) - 总体标准差\(\sigma\)已知 - 正态分布 |
评判两组样本平均数之间的差异程度 |
| T检验 | - Z检验改进版 - 小样本(样本容量<30)或大样本 - 总体标准差σ未知,用统计量S代替 - T分布,当数量足够大时是正态分布 |
比较样本和总体的差别 - 评判两组样本平均数之间的差异程度:用标准正态分布的理论来推断差异发生的概率,从而对两个平均数的差异进行比较,判断该差异是否显著 |
| 卡方检验 | 略 | 检验两个变量之间有没有关系 |
| F检验 | 略 | 检验方差是否有显著性差异 |
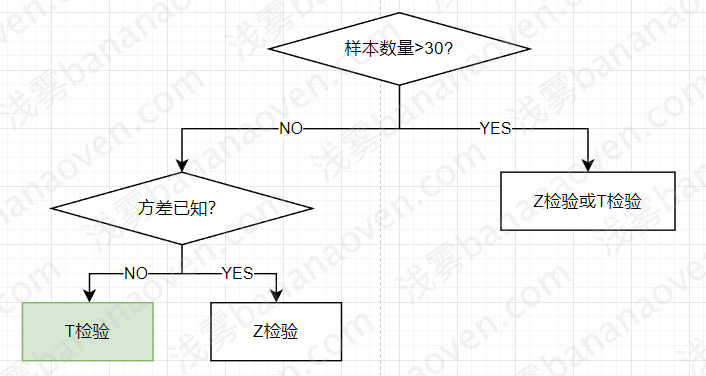
我们应该使用T检验或Z检验,但通常情况下,总体标准差都是未知的,因此只能使用T检验。
为了简化,我们将小样本(<30)直接判定为结果不可信,只用T检验处理大样本的情况,即近似正态分布的情况。
T检验的原理
我们的目的是为了比较\(\mu_1\)和\(\mu_2\)。当从一个正态分布N(\(\mu\), \(\sigma^2\))中抽样,抽样分布为N(\(\mu\), \(\frac{\sigma^2}{n}\))。我们两个实验桶都是抽样分布,因此:
| 分桶 | 均值 | 方差 |
|---|---|---|
| 300-30 | \(\mu_1\) | \(\frac{\sigma_1^2}{n_1}\) |
| 100-10 | \(\mu_2\) | \(\frac{\sigma_2^2}{n_2}\) |
为了比较\(\mu_1\)和\(\mu_2\),我们将两个分布相减,产生一个新的正态布N(\(\mu_1-\mu_2\), \(\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}\))。这样,我们可以把这个分布和标准正态分布N(0, 1)进行比较,也就是把这个正态分布转换为标准正态分布,然后将其值和标准正态分布取值进行比较,这个值就是t值:
$$ t = \frac{(\bar{x_1}-\bar{x_2})-(\mu_1-\mu_2)}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}} $$
其中,由于\(\sigma_1\)和\(\sigma_2\)未知,使用的是统计量\(S_1\)和\(S_2\)代替(并不是直接替换,数学过程复杂,略)。
根据我们的原假设,\(\mu_1=\mu_2\),因此t统计量公式简化为:
$$ t = \frac{(\bar{x_1}-\bar{x_2})}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}} $$
如果是符合原假设,那么这个t值应该无限接近于。t值偏大、偏小都应该是小概率事件。我们以标准正态分布代替t分布,然后画出95%的区域,即\(\alpha\)=5%,就可以认为,我们有95%的把握认定t值应该出现在包含0值的95%的分布范围内。
- 如果t值出现在95%区间以内,就接受原假设
- 否则就接受备择假设:
- 如果t值上下限都在右侧(正值),则接受备择假设中的\(\mu_1>\mu_2\),正向显著
- 如果t值上下限都在左侧(负值),则接受备择假设中的\(\mu_1<\mu_2\),负向显著
- 其他情况则是\(\mu_1\neq\mu_2\)
我们标准化一下:
- 当t落在右侧拒绝域,即\(t≥t_\frac{\alpha}{2}\)时,说明实验结果是正向统计显著;
- 当t落在非拒绝域,即即\(-t_\frac{\alpha}{2}<t<t_\frac{\alpha}{2}\)时,说明实验结果是非统计显著;
- 当t落在左侧拒绝域,即\(t≤-t_\frac{\alpha}{2}\)时,说明实验结果是负向统计显著;
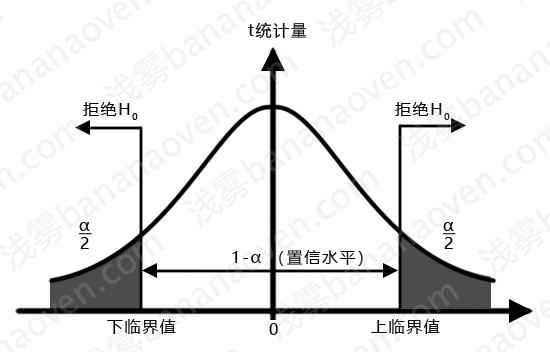
例如,当\(\alpha\)=0.05时,查询标准正态分布表可知\(t_\frac{\alpha}{2}\)=1.96,如果t=3.297>\(t_\frac{\alpha}{2}\),则我们认为是正向显著的。
两类错误
(1) 第1类错误,也叫\(\alpha\)错误,弃真错误等。
\(\alpha\)是一个概率值,表示原假设为真时,拒绝原假设的概率,也称为抽样分布的拒绝域。在这两类错误中,相对更加严重的是第1类错误,所以\(\alpha\)的取值应尽可能小。常用的\(\alpha\)值有0.01,0.05,0.10,由试验者事先确定。对比试验中使用的\(\alpha\)值通常是0.05(5%),这是显著性检验中最常用的小概率标准值。
(2)第2类错误,也叫\(\beta\)错误,取伪错误等。
| 接受\(H_0\) | 拒绝\(H_0\) | |
|---|---|---|
| \(H_0\)为真 | \(1-\alpha\) 正确决策 | \(\alpha\) 弃真 |
| \(H_0\)为伪 | \(\beta\) 取伪 | \(1-\beta\) 正确决策 |
样本量一定时,\(\alpha\)和\(\beta\)是此消彼长的关系。
- 置信度水平=\(1-\alpha\),不犯第1类错误的概率,通常取95%
- 统计功效=\(1-\beta\),不犯第2类错误的概率,通常定义在80%(\(\beta<0.2\))以上
另外,单独的\(\alpha\)又被称作“显著性水平”
P值
P值是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。
如果P值很小,说明这种情况发生的概率很小,而如果出现了,根据小概率原理,我们就有理由拒绝原假设,P值越小,拒绝原假设的理由就越充分。
P值的计算是由Z统计值的值转换而来,和显著性的关系:
- \(p≤\alpha\):说明实验结果是统计显著的
- \(p>\alpha\):说明实验结果是非统计显著的
置信区间
置信区间就是用来对一个概率样本的总体参数的进行区间估计的样本均值范围。置信区间展现了这个均值范围包含总体参数的概率,这个概率称为置信水平。置信区间就是我们想要找到的这么一个均值区间范围,此区间有95%的可能性包含真实的总体均值。
根据统计学的中心极限定理,样本均值的抽样分布呈正态分布。因此,通过相关的公式我们可以计算出两个总体均值差的95%置信区间。
总结检验公式
| 指标类型 | 数学期望 | 方差 | t统计量 | 置信区间 |
|---|---|---|---|---|
| 均值 | \(\mu_1-\mu_2\) | \(\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}\) | \(t=\frac{(\bar{x_1}-\bar{x_2})}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}\) | \((\bar{x_1}-\bar{x_2})±t_\frac{\alpha}{2}\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}\) |
| 比例 | \(\pi_1-\pi_2\) | \(\frac{\pi_1(1-\pi_1)}{n_1}+\frac{\pi_2(1-\pi_2)}{n_2}\) | \(t=\frac{p_1-p_2}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}}\) | \((p_1-p_2)±t_\frac{\alpha}{2}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\) |
四、样本选择
辛普森悖论
当人们尝试探究两种变量是否具有相关性的时候,会分别对之进行分组研究。然而,有时候会发现在分组比较中都占优势的一方,在总评中有时反而是失势的一方。
| 300-30优惠券,下单率 | 100-10优惠券,下单率 | |
|---|---|---|
| 女生 | 38/80=47.5% | 14/20=70% |
| 男生 | 2/20=10% | 16/80=20% |
| 所有人 | 40/100=40% | 30/100=30% |
例:假设研究300-30和100-10优惠券和下单率关系,分开男生和女生进行统计,然后合
并统计。
从分开的统计可以看出,无论是男生还是女生,似乎都更喜欢使用100-10优惠券下单。然而从总的统计,却发现300-30优惠券下单率更高。
到底哪个结论是正确的呢?都不正确。
在这个实验中,可以明显看到,无论用哪种优惠券,女生下单率都比男生高。而女生中,统计300-30的总人数是80人,统计100-10的总人数是20人。也就是在“下单率高的人群中”(女生),300-30的样本数远高于100-10的样本数,这才导致了总体上300-30比100-10的下单率更高。
为了避免辛普森悖论影响,我们要这样做:
- 划分样本时,注意总体样本的均匀性,不要出现A桶1个样本,B桶10000个样本
- 划分样本时,注意各维度样本的相似性,比如男女分类去观察时,不要出现A桶女生80男生20,B桶女生20男生80的情况
最小样本量
如果样本量太小,那么实验结果就不会可信。比如统计下单率,只看1个人的数据,就说实验结论,肯定不可信。如果样本量太大,影响面也会很大,对于一些探索性质实验,有可能会影响用户体验,造成用户流失。
所以选择一个合适的样本量很重要,那么怎么确认所需的样本量呢?
样本量的四个影响因素:
- 显著性水平\(\alpha\):显著性水平是犯第一类错误的概率,这个值越低,对实验结果的要求越高,越需要更大的样本量
- 统计功效\(1-\alpha\):统计功效意味着避免犯二类错误的概率,这个值越大,需要的样本量也越大
- 差异变化\(E=\mu_1-\mu_2\):差异越小,需要的样本越大
- 标准差\(\sigma\):标准差越大,代表两组差异的趋势越不稳定,需要的样本量越大
最小样本量计算公式:
$$ n = \frac{\sigma^2}{E^2}(t_\frac{\alpha}{2} + t_\beta)^2 $$
其中,\(\sigma\)我们是很难得到的,因此需要进行估计(并不是直接替换,数学过程略过)。
- 两均值之差:
- \(\sigma^2=S_1^2 + S_2^2\)
- \(E=\bar{x_2}-\bar{x_1}\)
- 两比例之差:
- \(\sigma^2=p_1(1-p_1)+p_2(1-p_2)\)
- \(E=p_2-p_1\)
于是,对于比例,公式可以简化为:
$$ n = \frac{2p_1(1-p_1)}{E^2}(t_\frac{\alpha}{2} + t_\beta)^2 $$
假设选择通用显著性水平\(\alpha\)=5%,统计功效\(1-\alpha\)=80%,我们实验的目标是“分享率”,其值为10%,预期实验桶会提升1%,则通过上述样本计算公式可以得出最小样本量:
$$ n = \frac{2\times10\%\times(1-10\%)}{1\%^2}(1.96 + 0.84)^2=14112 $$
五、分流算法
我们需要根据配置的百分比,将实验对象均匀地分到各个实验桶中,需要一种分流算法。
| 实验桶 | 流量 |
|---|---|
| 用户将看到300-30的优惠券 | 50% |
| 用户将看到100-10的优惠券 | 50% |
1、完全随机 CR(Complete Randomization)
直接根据分流key进行哈希,比如分流key是userId,那么用户请求就会进入hash(userId)%2的桶。
哈希算法有很多:
- 适用范围很广的经典算法:MD5、SHA
- 相似文本输出相似哈希值的特征提取算法:simHash
- 地理位置特征哈希算法:geoHash
- 均匀分布哈希算法:murmurHash
- 新的快速算法:cityhash
- ……
AB实验选择哈希算法的标准是:
(1)能够通过卡方测试:给出大量的数据,利用哈希函数计算出他们的哈希值,期望得到
的哈希值是均匀分布在哈希空间的。比如这里有2个实验桶,分流key是userId,流量比例
是1:1,那么期望userId应该被均匀地分入两个桶中,50万用户进入A桶,50万用户进入B
桶,而不是一个桶1万用户另一个桶99万用户。
(2)能够通过雪崩测试:给出较小的输入变化,哈希值会产生巨大变化,像是随机一样。
因为通常我们分流key都是userId这种连续增长的值,用户A是1000000,用户B是
1000001,输入值差距就会很小。如果他们哈希之后仍然很相似,那么大概率会被划分到
同一个桶中,这样就会出现“userId号码相近”用户落入同一个桶的现象,样本就不是互相
独立的了,我们需要去掉这个限制,微小差异输入应当产生巨大差异输出。
符合这2个条件的,只有MurmurHash。通常,我们选择最新的MurmurHash3。
murmurHash算法已被广泛应用于许多开源项目中,如Redis、Perl、Nginx、Memcached、HBase、Hadoop、ElasticSearch等。由于它优秀的性能和均匀的分流能力,murmurHash常常被用于A/B测试平台中。
我们可以看一组MurmurHash分桶数据,可以明显看出,样本量在10000以上,分桶就已经十分均匀了:
| 样本量 | 桶1 | 桶2 | 桶3 | 桶4 | 最大分桶差 |
|---|---|---|---|---|---|
| 1000 | 25.7% | 23.6% | 23.8% | 26.9% | 1.9% |
| 10000 | 24.97% | 25.06% | 24.38% | 25.59% | 0.62% |
| 100000 | 24.929% | 24.961% | 24.985% | 25.125% | 0.125% |
| 1000000 | 25.058% | 24.941% | 24.988% | 25.013% | 0.058% |
2、多次随机 RR (Rerandomization)/SeedFinder
直接CR,仍然有概率会分流不均匀,所以可以这样做:先把两个桶都设置成相同分桶,比如都是“100-10”,如果发现分流后数据不均匀,则重新分流;如果均匀了,再利用分好的数据进行AB实验。
进一步地,我们可以标准化这个过程:进行最多1000次重复模拟分流,每次分流选取不同的随机种子,分流完成后用一个“均匀函数”去评判数据均匀程度,直到均匀程度达到预期,再开始AB实验。
这种方式只能用于离线AB实验。
3、自适应分组
进行多次分配,根据已分配和待分配的样本分布,自适应地调整下一次分配的策略。
比如:
(1)先给每个桶分10个人
(2)计算桶的分布情况,如果类似,则继续均匀分配;如果有巨大差异,则反向调节,让其再下次分配中达到平衡。
这种方式只能用于离线AB实验。
4、分层抽样
如果我们已经知道用户的分层,那么完全可以A桶每个分层抽样N个,B桶每个分层抽样N个,来完美地均匀。
这种方法需要非常注意实验的目的,比如我们的目标是“优惠券面额和下单行为”,但我们分层的标准是“用户的身高”这种完全无关的分层,就没有意义,更好的分层标准应该是适配目标的,比如“用户历史领取优惠券和下单行为”。
5、完美匹配
如果在A桶放入一个A用户,那么就给B桶匹配一个和A用户几乎完全一样的B用户,这样也能均匀。
困难可能在于,世界上不会有2个完全相同的人,而且为了“匹配”,我们需要在无数个维度上进行比对,陷入维度灾难。所以实际操作上,通常需要进行特征提取和降维。
总结
| 分流算法 | 速度 | 在线 | 离线 | 效果 | 备注 |
|---|---|---|---|---|---|
| CR | 快 | 支持 | 支持 | 一般 | 简单 |
| RR | 一般 | - | 支持 | 好 | 重复次数足够多,就会足够均匀 |
| 自适应 | 慢 | - | 支持 | 好 | 只分一次的情况下,分流效果好 |
| 分层抽样 | 一般 | - | 支持 | 一般 | 简单 |
| 完美匹配 | 慢 | - | 支持 | 好 | 只分一次的情况下,分流效果好 |
通常,我们都是在线AB,所以一般选择CR的Murmurhash3。
六、分流实现
1 | public Integer hash(String key, String salt) { |
这里有很多细节:
1、每个实验,都有唯一的salt值,保证无论多少次哈希,得到的结果都是一致的。
2、不同实验,具有不同的salt值,保证在key相同的情况下(通常key都是userId),进行不同实验,能有机会哈希到不同的桶中。
3、如果是联合实验,比如“命中实验1-A桶的用户,必须命中实验2-A桶”,那么只需要简单设置相同的salt值就可以实现。
4、Murmurhash3后得到Long,我们只需要取整再取余,就能直接得到哈希到的分桶ID了。这个取余的值很关键,比如100W就表示我们有100W个哈希桶,这决定了我们AB实验桶的个数最多是100W个,同时决定了流量粒度最小单位是0.0001%
| 分桶 | 流量 | 本质上对应哈希桶 |
|---|---|---|
| 桶0 | 0.0001% | 第0个桶 |
| 桶1 | 99.9999% | 第1个桶~第999999个桶 |
| 分桶 | 流量 | 本质上对应哈希桶 |
|---|---|---|
| 桶0 | 0.0001% | 第0个桶 |
| 桶1000000 | 0.0001% | 第999999个桶 |
七、流量调整
1、串桶的危害
串桶是指,用户A本来是属于桶A的,但由于流量调整,又被重新分配到了桶B。
假设桶A是“展示300-30优惠券”,桶B是“展示100-10优惠券”,那么用户可能发现,今天看到了“300-30”优惠券,明天又看到“100-10”,会引起迷惑;同时数据统计时,A用户的下单行为,到底是因为300-30还是100-10呢?进一步,假设不是展示,而是领取,那么用户就能今天领“300-30”,明天领“100-10”,产生资损!
2、流量调整策略
实验过程中,是可以调整流量的。调整时,哈希桶是如何变化的呢?
| 方法 | 例子 | 操作 |
|---|---|---|
| 增加流量 | 10%流量 -> 20%流量 | 增加对应哈希分桶,数据无串桶 |
| 减少流量 | 20%流量 -> 10%流量 | 减少对应哈希分桶,数据无串桶 |
| 增加流量同时减少流量 | A桶:50%流量 -> 30%流量 B桶:50%流量 -> 70%流量 |
数据存在串桶行为! A桶的20%流量变到B桶中 |
一边增加一边减少,串桶不可避免。
3、从实验设计上规避串桶
我们只能从实验设计上去规避串桶。
| 方法 | 操作 |
|---|---|
| 同等扩大法 | - 对照组:5%->10%->50% - 实验组:5%->10%->50% 需要在放量至50%的时候得出结论,不可再调整流量比例。 |
| 对照组固定比例 | - 对照组:5%->5%->5% - 实验组:5%->10%->15%->95% 需设置兜底方案 |
| 固定观测 | - 对照组:50% - 实验组:50% |
八、A/A实验
通常,我们实验都会有一个参照桶(代表了什么都不做的当前现状),称之为“对照组”。通过对比“实验组”和“对照组”的数据,来验证“实验组”的调整是否有正向效果。
所以,A/A实验是指,同时开2个以上相同效果的分组,测试实验结果是不是因为“分桶不均”产生的,而不是“实验调整”产生的。
比如:
- A1:100-10优惠券 - 下单量
- A2:100-10优惠券 - 下单量
- B1:300-30优惠券 - 下单量
- B2:300-30优惠券 - 下单量
理论上,效果A1=A2,效果B1=B2,如果出现明显不一致,说明这个实验不可信,分桶不均匀。
此时就应该去做检查:
- 实验流量是否小于1万?数量太小,分布不均
- 实验流量是否被其他策略污染过?比如有的用户提前得到了红包,导致下单量增加,而不是优惠券产生的效果。
- 是否存在异常值?比如有一个用户是富豪,下了巨多单,导致整体下单量增加
A/A实验是个好习惯吗?
不一定。
(1)AABB会浪费流量。本来50%、50%,变成了25%、25%、25%、25%
(2)犯错概率增加。本来2组对比,犯一类错误概率是5%,如果4组对比,那么概率变成(1-\(0.95^4\))=18%,大大增加。
采用A/A实验,需要看场景。通常情况下,我们是不会做AA实验的,除非你明确知道可能有策略污染、异常值之类的问题。
九、实验指标
1、指标设计
我们应该观测哪些指标,以确定实验结果?
- 核心指标/评价指标:实验目的中需要提升/降低的指标,一般不超过3个。
观测目的:确定实验结论
比如:下单率提升、分享率提升、点击率提升、退货率下降 - 全局指标:所有实验都必须关注的指标。
观测目的:确定实验不会对总体有较大负面影响
比如:商品交易总额、日活跃用户数量 - 护栏指标:实验不应该影响的指标。
观测目的:确定实验没有出现预期外的负面影响
比如:页面跳失率、APP卸载率、账号注销率 - 其他指标:其他你需要的过程指标。
观测目的:更好地描述和解释实验结果
比如:核心指标是“分享率”,但你同时也想知道“分享人数”和“总人数”,那么就可以作为过程指标。
常见观测指标:
- UV:Unique Visitor,独立访客。一个客户端为一个独立访客。
- PV:Page View,页面浏览量。同一用户多次访问,累计。
- PDP:Product Detail Page,商品详情页。
- DAU:Daily Active User,日活跃用户数量
- WAU:Weekly Active Users,周活跃用户数量
- MAU:Monthly Active User,月活跃用户数量
- BR:Bounce Rate,跳失率,是指显示顾客通过相应入口进入,只访问了一个页面就离开的访问次数占该页面总访问次数的比例
- DAB:Daily Active Buyers,日活跃买家数量
- GMV:Gross Merchandise Volume,商品交易总额(一定时间段内),多用于电商行业,一般包含拍下未支付订单金额
- ROI:Return on Investment,投资回报率。ROI=收益/成本
- ATC、A2C:Add to Cart,用户把商品加入购物车
- CAC:Cost per Acquired Customer,每获得一个买家用户,需要付出的成本。CAC=成本/新买家数量
2、指标显著性
p值和显著性的关系:
- 当p<=0.05时,说明实验结果是统计显著的,即拒绝原假设;
- 当p>0.05时,说明实验结果是非统计显著的,即接受原假设
置信区间和显著性的关系:
- 如果置信区间同为正,说明实验结果是正向统计显著的,即拒绝原假设;
- 如果置信区间同为负,说明实验结果是负向统计显著的,即拒绝原假设;
- 如果置信区间为一正一负,说明实验结果是非统计显著的,即接受原假设
有时候,我们会发现,提升多不显著,提升少却显著:
| 实验A指标1 | 实验B指标2 |
|---|---|
| +10.03% 不显著 | +0.03%显著 |
因为显著性和绝对值并没有绝对关系,只和p值和置信区间有关。不用在意绝对值。
指标按照显著性通常分为:
- 需要正向提升的指标:分享率、下单率、成功率
- 需要负向提升的指标:错误率、失败率
通常情况下,我们把所有指标都设置为正向提升。比如“错误率”、“失败率”都改为“成功率”,方便理解。于是,实验目标设定与结论为:
- 如果指标正向显著,且提升幅度达到实验目标,则可以直接推全;
- 如果指标正向显著,但提升幅度未达到实验目标,则可以结合业务需要决定是否推全;
- 如果指标不显著,但提升幅度达到实验目标,则样本量不足,需持续观察一段时间;
- 如果指标负向显著,则建议立刻停止实验
我们以一个实际例子来分析显著性:
- A桶分享率为22%,采样样本数量为149617
- B桶分享率为28%,相比于A桶提升了(0.28-0.22)/0.22=27.27%,采样样本数量为157627
- \(\alpha\)为5%
代入前面比例置换区间的公式:\((p_1-p_2)±t_\frac{\alpha}{2}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\)
可以求得:\((28\%-22\%)±1.9616\sqrt{\frac{28\%(1-28\%)}{157627}+\frac{22\%(1-22\%)}{149617}}\)
即:0.06±0.003055=[0.056945, 0.063055]
再除以对照组A桶的值22%,我们可以得到置信区间取值:[25.88%, 28.66%],上下限都在22%的右侧,说明小概率事件发生了,而且是正向显著。
从而得到实验结论:如果用实验桶B的方案,能使分享率相比原来提升27.27%
3、核心指标越多越好?
不是,最好是1个,一般不超过3个。因为:
- 一次检验过程围绕单个指标进行,如果是多个指标则需要多次检验,增大了犯一类错误的概率
- 多个指标需要评估多分最小样本量,取最大值。这点容易被忽略。
十、新奇效应和实验时间设定
新奇效应:指的是对于产品上的一个新样式、新功能、新模块等,用户出于新鲜感产生更多的行为,而导致指标出现正向提升的情况,这种提升并非是实验要测试的新样式、新功能、新模块带来的,随时间拉长会逐渐消失。
为了避免因新奇效应而误判,我们的实验时间通常需要在7天以上。
十一、多重检验问题MTP
经典场景:常规AB桶实验,进行了14天,前面13天指标增长都不显著,已经基本判定为实验失败,但到了第14天突然显著。
1、多重检验问题
这就是多重检验问题MTP(Multiple Testing Problem),又叫多重测试问题或多重比较问题,指的是当同一时刻比较多个检验时,第一类错误a就会增大,而实验结果的准确性就会受到这个影响。
通常一个检验中,我们犯第1类错误的概率是\(\alpha\)。如果发生N次检验,那么在这N次检验中,至少出现第一类错误的概率是:\(P_{至少出现第1类错误}=1-(1-\alpha)^N\)。比如\(\alpha\)=5%,N=30,那么犯错概率会从5%提升到78.5%。
2、多重检验出现场景
(1)进行多桶实验
比如前面提到的A/A实验。
- A1/A2/B实验,进行了A1-B、A2-B的2次检验。
- A/B1/B2实验,进行了A-B1、A-B2的2次检验。
(2)具有多个核心指标
比如前面提到的指标问题,会产生多次检验。
(3)多维度分析实验
比如对于实验结果,我们再细分了“10-30岁”、“30-100岁”等人群分别去分析,也会产生多次检验。
(4)多次查看实验结果
比如这里的经典场景,9天实验,前面8天每天都去运行一次结果,每次运行都会产生一个检验。
3、如何解决多重检验问题
1、样本量达到“最小样本量”后,再去运行实验结果,否则不可信。
2、p值不变,调整\(\alpha\)。
也就是Bonferroni Correction方法,调整\(\alpha\)值为\(\frac{\alpha}{N}\)。比如有30次检验,那么就把\(\alpha\)设置为5%/30=0.1,那么\(P_{至少出现第1类错误}=1-(1-\alpha)^N\)=4.76%,和预期的5%接近。适合检验次数N不多的场景。
3、\(\alpha\)不变,调整p值。当维度较多,使用BC方法减少\(\alpha\),会导致第2类错误\(\beta\)显著增加,此时需要使用 FDR (False Discovery Rate)方法,其中常用的是BH法,原理复杂,略。
十二、异常值处理
异常值对指标影响很大,容易导致我们误判实验结论。比如下单量,如果有一个氪金大佬下巨多单,会导致均值提升影响判定。
我们可以用偏度和峰度来描述数据分布形态。
(1)偏度(skewness)是指数据分布的偏斜程度,即数据分布的不对称程度。当偏度为0时,数据分布为对称分布;当偏度为正数时,数据分布向右偏;当偏度为负数时,数据分布向左偏。
$$ SK_1 = \frac{m_3}{m_2^\frac{3}{2}} = \frac{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^3}{[\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2]^\frac{3}{2}} $$
(2)峰度(kurtosis)是指数据分布的峰态程度,即数据分布的尖锐程度。当峰度为0时,数据分布为正态分布;当峰度为正数时,数据分布的峰比正态分布更尖:当峰度为负数时,数据分布的峰比正态分布更平坦。
$$ g_2 = \frac{m_4}{m_\frac{3}{2}}-3 = \frac{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^4}{(\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2)^2}-3 $$
为了减少异常值对实验结果的影响,通常会在计算指标值之前,且数据峰度>50时,将0.05%的极大值判定为异常值直接丢弃。但不处理极小值,因为对于“提升指标”,极大值会影响判断;对于“降低指标”,极小值属于真的有问题需要分析的。
十三、实验结论一定正确吗
不一定。当我们发现实验结果显著,推全放量后,却发现效果不佳,很可能因为:
- 结论正确,统计显著,但实际提升效果较小,所以不明显
- 结论错误,恰好命中5%的第1类错误(去真),导致执行了错误的方案
不过,根据AB实验结论选择方案,一定比拍脑袋的方案错误率更低。如果错了,改正就完事了。

