毕业设计整理（六）：LBP纹理特征

局部二值模式（Local Binary Pattern，LBP）是一种用来描述图像局部纹理特征的算法，反映的是图像像素点周围纹理变化情况，具有旋转不变性、灰度不变性（光照变化无影响）、计算复杂度低等优点，1994年首次由Timo Ojala, Matti Pietikainen等人提出，用于纹理特征提取。2002年论文《Multiresolution gray-scale and rotation invariant texture classification with local binary patterns》进行了归纳总结，2018年该论文引用量154次，累计9832次。

LBP特征描述

原始LBP特征

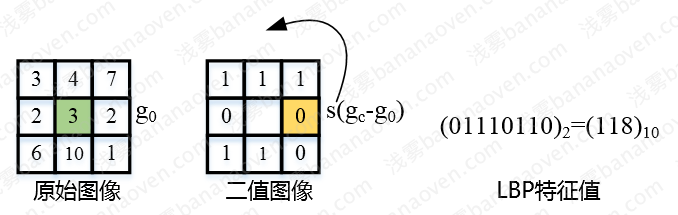
使用3×3矩形模板，从上到下，从左到右逐行扫描，模板中心像素值为\(g_c\)，从右侧中间像素点开始编号\(g_p(p=0,…,7)\)。每次周围像素与中心像素比较：

$$ s(g_0-g_c)= \begin{cases} 1& {g_0-g_c \ge 0}\\ 0& {g_0-g_c < 0} \end{cases} $$

得到二值图像，将二值图像值从右侧中间像素点逆时针排列，得到8位二进制数，转为10进制数，就是该中心点\(g_c\)的LBP特征值：

$$ LBP=\sum\limits_{p=0}^{7}{s(g_0-g_c)2^p} $$

一幅图像的LBP特征如果用灰度图形化显示出来就是这样的：

你可以用lbp的官方matlab代码|百度网盘（密码：3yzp） 去测试和实际使用：

• lbp.m - LBP returns the local binary pattern image or LBP histogram of an image.
• getmapping.m - GETMAPPING returns a structure containing a mapping table for LBP codes.
• cont.m - C computes the VAR descriptor.

详细描述和样例在头部注释里都有，这里给出我上面测试的例子：

function lbptest
     I=imread('rice.png');
     SP=[-1 -1; -1 0; -1 1; 0 -1; -0 1; 1 -1; 1 0; 1 1];
     I2=lbp(I,SP,0,'i');
     subplot(1,2,1)
     imshow(I)
     title("rice.png")
     subplot(1,2,2)
     imshow(I2)
     title("lbp特征")
end

LBP的整体思想非常简单，计算复杂度很低，反映的特征较好，但是有两个明显问题：

1. 3×3邻域模板过小，无法捕获大尺度纹理结构
2. 矩形模板是具有旋转不变性的

因此很多人开始改进。

圆形LBP特征：Circle LBP

在论文的2.1 Achieving Gray-Scale Invariance中，Ojala等人提出了圆形邻域系统，如下图所示，定义中心点为\(g_c\)，从最右中间点开始计数\(g_0-g_P-1\)共\(P（P>1）\)个点，它们等角均匀地分布在半径为\(R（R>0）\)的圆周上。以\(g_c\)为原点（0, 0），圆周上的点\(g_p\)坐标为\((-Rsin(2πp/P), Rcos(2πp/P))\)，如果点没有落到像素中心，则采用插值的方式进行估计近似，通常来说使用双线性插值。

这样就可以通过改变P的值在圆上添加任意多个点，也可以通过改变R的值任意改变模板大小，记这样的LBP算子为：

$$ LBP_{P,R}=\sum\limits_{p=0}^{p-1}{s(g_0-g_c)2^p} $$

然而圆形LBP依然不具有旋转不变性。

旋转不变LBP特征：LBPROT

我们总是选择最右中间点作为起始点\(g_0\)，所以当LBP算子旋转的时候，\(g_0\)会发生变化，这样即使是同一个模板、同一个位置、同样的P、R，计算得到的LBP特征值都是不同的。为了消除这种旋转差异，在论文的2.2 Achieving Rotation Invariance中，作者重新定义了LBP计算方式：

$$ LBP_{P,R}^{ri} = min\{ROR(LBP_{P,R}, i)|i=0,1, ..., P-1\} $$

其中\(ROR(x,i)\)指的是对p位数字x进行i次循环右移。也就是说，从各个旋转的LBP二进制串中，找到最小的值，作为这个模板的LBP特征。举个例子，假设P=8，R=1（8个点，半径1），那么对于4个连续的1，4个连续的0（00001111）来说，可以旋转的有：

显然最小的是15，所以这个模板的值就是15。

看起来圆形LBP很完美，但实际使用发现LBPROT并不具有很好地辨别力，因为随着采样点数的增加，二进制模式会急剧增多，会使得数据量过大，直方图过于稀疏，不能很好地反映图像特征。

等价LBP特征：Uniform LBP

针对圆形LBP缺点，作者在2.3 Improved Rotation Invariance with “Uniform” Patterns and Finer Quantization of the Angular Space中进一步提出等价LBP特征，利用等价模式来对LBP模板种类进行降维。我们首先定义“跳变”为二进制串中”01”、”10”这样的变化，定义等价量度（Uniformity measure U(“pattern”)）为二进制串中的跳变次数。Ojala等人发现，大部分图像中都只包含两次跳变，于是可以保持跳变次数小于等于2的模式不变， 大于2的模式笼统归为归为一类。定义LBP：

$$ LBP_{P,R}^{riu2} = \begin{cases} \sum_{p=0}^{p-1}{s(g_p-g_c)}& {U(LBP_{P,R}) \le 2}\\ P+1& {otherwise} \end{cases} $$

其中，

$$ U(LBP_{P,R})=|s(g_{P-1}-g_c)-s(g_0-g_c)|+\sum_{p=0}^{P-1}{s(g_p-g_c)-s(g_{p-1}-g_c)} $$

例如，(00000000)2 等价于 (11111111)2，他们的等价量度U都是0，没有跳变，它们都是小于等于2的等价模式类；而(10101010)2含有8次跳变（注意是循环计数的，头和尾的差异也算跳变），属于混合模式类。

我们以P=8，R=1来仔细分析，本来应该有2^8 = 256个模式，这样一划分就变成了：

等价量度	模式个数
U=0	2
U=1	0
U=2	56
U=3	0
U=4	140
U=5	0
U=6	56
U=7	0
U=8	2

共9种跳变，那么小于2次的共58种LBP模式，将其编码为1-58；其余的混合模式类统一编码为0，如果用灰度值图像展示等价LBP会发现这种LBP特征值图像偏暗，因为大部分不重要的特征像素都被编码为0=黑色了。

等价LBP将原来2^P指数个模式变为了P(P-1)+2多项式个模式，大大减少了内存占用，并且特征维度的降低可以减少高频噪声带来的影响。

等价LBP不具有旋转不变特性。

旋转不变等价LBP特征

将旋转不变的圆形LBP和等价LBP结合起来，就构成了最强功能的旋转不变等价LBP特征。将旋转不变LBP进一步分成P+1类均匀旋转不变模式和1类非均匀模式。实验表明，旋转不变均匀LBP具有最低特征维数，保持鉴别力的同时具有良好的旋转不变性和灰度不变性，是LBP中最好的特征了。

LBP特征提取方法

1. 提取整幅图的LBP特征
2. 将特征按相同规则转为向量，例如按行拼接，就能够进行后续处理了。

参考资料

1、《LBP(局部二进制模式)》
2、《LBP原理介绍以及算法实现》
3、《LBP特征原理及代码实现介绍》